Seabirds such as albatrosses and petrels soar over the Southern and Pacific Oceans using a technique known as dynamic soaring and it is thought that they are somehow using the wind gradient to achieve this. Here is a pilot’s perspective on an aspect of bird flight.
Avian soaring flight began to be studied in the 19th century and a form of dynamic soaring was first proposed by Lord Rayleigh in an article in Nature in 1883. The debate was initially about observations of pelicans thermal soaring and that kind of soaring has since been explained by other means and practised by glider pilots. The flight of the albatross remained to be explained. It was noted that albatross fly at low level where the wind gradient is found and so the
‘Rayleigh cycle’ of dynamic soaring appeared to be the answer. Rayleigh asserted that birds cannot soar in a uniform, horizontal wind, and people have been trying to explain dynamic soaring in terms of the wind gradient ever since.
It is assumed that if the bird glides downwind it can gain airspeed from the wind gradient and convert this excess kinetic energy (KE) to height in a zoom-climb. However, if wind-speed is converted to airspeed by transfer of momentum from air to bird most of the energy is going to be lost due to drag which increases with the square of the airspeed. Although the bird can convert excess airspeed to height it cannot, because of drag losses, return to its starting height. Put another way, if the increase in airspeed in the dive is the same as the loss of wind speed in the wind gradient, then KE is the same at the bottom of the dive as at the top. There is no gain of energy, only a more rapid loss of height.
The new Windward Turn theory of dynamic soaring is derived from an analysis of kinetic and potential energies during the kind of manoeuvres that albatross are seen to perform. Here’s how it works: In a windward turn at constant airspeed, height energy is gained from wind energy due to a decreasing tailwind/ increasing headwind component. The energy exchange is facilitated by an inertial force, analogous to thrust, derived from the rate of change of momentum due to the reducing ground speed. In a leeward turn, height energy is lost due to a decreasing headwind/ increasing tailwind component. The rate of change of momentum is reversed but losses are minimised by flying the leeward turn in a steeply inclined plane at reduced airspeed. Provided that the bird gains more height energy in the windward turn than it loses in the leeward turn then it can maintain or gain height. See figure 1.
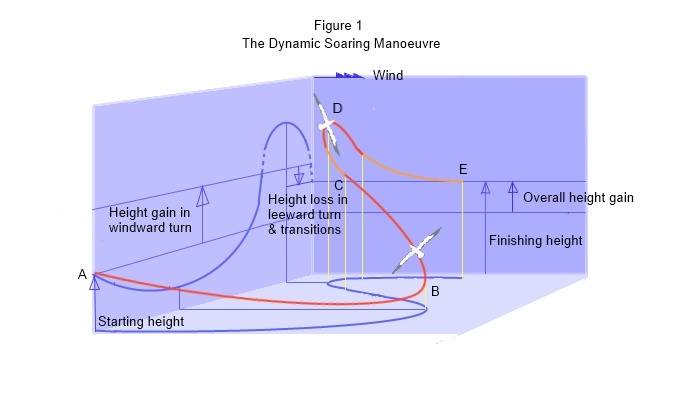
Airspeed is the same at the beginning and end of the windward turn, but kinetic energy at the beginning of the turn is proportional to airspeed plus tailwind component (squared) and at the end of the turn is proportional to airspeed minus headwind component (squared). The loss of kinetic energy enables a gain of potential energy. As the bird comes around into wind, still at best glide speed (point C), the bird keeps climbing and now reduces airspeed (orange line) and turns the other way. Now at about half best glide speed and a steep angle of bank but at low G and therefore with much reduced drag, it turns across the wind (point D) and dives at some angle to the wind, now with a tailwind component. Having completed the leeward turn at reduced airspeed the bird now trades some height for airspeed (orange line) before commencing the next windward turn.
At the beginning of this leeward turn, kinetic energy is proportional to airspeed minus wind component (squared) and at the end of the turn is proportional to airspeed plus wind component (squared) . At the end of the downwind turn, kinetic energy is greater and therefore height (potential energy) is lost. The mechanism of transfer of momentum is the reverse of that in the windward turn.
The bird can maintain height using dynamic soaring but can only do so at the expense of drifting downwind. This is probably why albatross circumnavigate the Antarctic continent with the prevailing wind. Provided that the energy transfer in the windward turn, is at least equal to the rate of loss of energy due to drag then the bird will maintain airspeed and maintain or gain height but only until the turn is complete.
The Windward Turn theory shows how dynamic soaring can work but contradicts most previous work on the subject. It shows that there is a possible mechanism to exploit a uniform horizontal wind at any altitude and there is no need to invoke the wind gradient or high G manoeuvring or high airspeeds. It also shows that there is not enough kinetic energy in the wind gradient to account for dynamic soaring, that although dynamic soaring happens in the same part of the sky as the wind gradient, the wind gradient actually reduces the efficiency of the manoeuvre and that dynamic soaring probably works better over the oceans than over the land because the wind gradient is smaller and the wind is stronger and steadier. It also helps to explain some aspects of bird physiology such as tube nostrils and high aspect ratio wings and of behaviour such as the direction of large scale flight patterns and the shape of small scale repetitive turns and also why the bird’s metabolic rate is low whilst gliding, because the manoeuvre is carried out at relatively low G. There is a more detail in the website.
Related links
Image credit: Black-footed Albatross © Bill Boulton
Blog with #theBOUblog
If you want to write about your research in #theBOUblog, then please see here.




